Designing Network Design Spaces

这篇论文给我感觉是很惊艳，实验表格真的是太充分了，而且不像EfficientNet那种大力出奇迹的感觉，这篇论文手工设计出了比EfficientNet还好的论文，经过我自己的实验。同样的epoch和batch size下，RegNetX-8.0GF只占用9G显存，9个半小时单卡就训练完了。但是efficientnet-b4占用双卡，显存占满，需要训练21个小时。最终两者的精度基本一致，但是推理时间RegNetX-8.0GF（15.65）只有efficientnet-b4（29.17）的一半。下面对该论文进行详细介绍。

创新点

提出了一个新的网络设计范例。以统计学的角度提高了对网络设计的理解，并探讨不同设置下的通用网络设计原则。作者不是专注于设计某个具体的网络，而是design network design spaces。整个过程类似于经典的手工网络设计，但是提升到了设计空间的层次。
使用所提方法，得到了包含一系列简单、常规网络模型的低阶空间——RegNet。在这个空间中，表现优异的网络的宽度和深度能够被一个线性函数量化。并且发现了一些和现有设计思想相悖的结论。
在不同的FLOPs约束下，都可以从RegNet设计空间中得到简单且轻量的模型。在相同的FLOPs和训练参数下，RegNet模型比EfficientNet的性能更好且在GPUs最多提速5倍。

创新点来源

传统NAS方法这种基于个体估计（individual network instance）的方式（每次评估的时候采样一个网络）存在以下缺陷：

非常不灵活（包含各种各样的可调参数）
泛化能力差（搜索出的网络可能跟特定设置有关，例如硬件平台）
可解释性差，不能发现网络设计原则，从而泛化到新的设置中

面对这个问题，作者提出了可以对网络设计空间进行整体估计（population estimation，意思就是所有的深度宽度之类的最佳设计空间关系给它估计出来）。直观地，如果能得到深度(depth)，宽度(width)等一系列网络设计要素关于网络设计目标的函数关系，那么就很轻松地知道大概多深、多宽的网络是最佳选择。那么也就可以解决上面所提的问题了，并且这个方式实际上能反应出更优的网络设计准则，从而达到作者Designing Network Design Spaces的目的。

Design Space Design

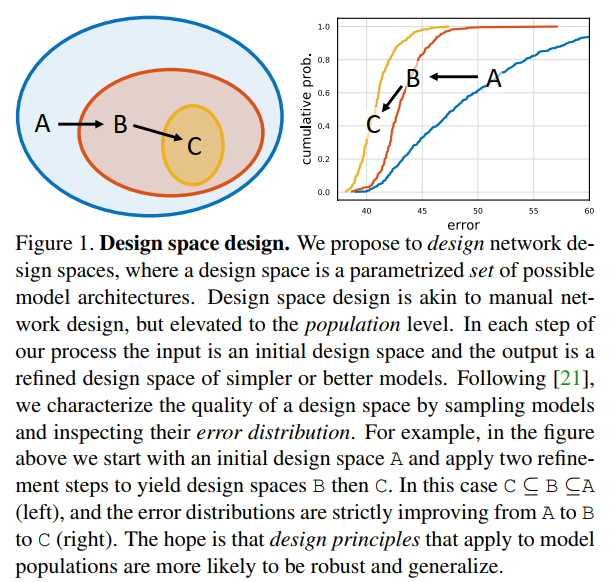
Design space（设计空间）是包含是一大群（可能是无限的）模型的空间。不同于search space（搜索空间），作者并不是在一个空间内搜索出一个具体的网络实例，而是设计空间本身。作者从一个初始的、不受约束的设计空间出发，通过发现的网络设计准则逐渐的简化该空间，称这个过程为design space design，如图1所示。可以看到这个过程类似于设计一个具体的模型，但是作者把它上升到了整体水平。

Tools for Design Space Design

那么如何评价一个设计空间的好坏呢？根据前人的研究，可以从设计空间中采样出一系列的模型，然后画出这一系列模型的误差分布图，以这个错误分布图来表征整个设计空间的好坏，直观上比在设计空间中搜索出最优模型然后比较这样的方式更加鲁邦且信息量更加充足。

具体而言，作者从一个设计空间中采样$n$个模型，然后对这$n$个模型进行一个low-compute、low-epoch的训练，即使用400M FLOPs（$10^6 $FLOPs，记作MF）的模型，且只在ImageNet上训练10个epoch。这样的实验很快速，训练100个400MF的模型10个Epoch和训练单个4GF（$10^9$ FLOPs，记作GF）的ResNet-50模型100个Epoch计算量大致相同。

作者主要靠the error empirical distribution function (EDF) 来评估一个设计空间的质量。第$i$个模型的误差记作$e_i$，则这$n$个模型的EDF计算公式为：

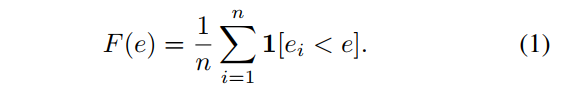
$F(e)$给出了误差小于$e$的模型占比。某个设计空间的EDF如图2(左)所示，可以看到通过这种方式能够将一个复杂的、高维设计空间的表现投影到一个二维空间，从而帮助我们更好的理解设计空间。在这些图中，作者使用了empirical bootstrap来评估最优模型的可能范围，如图2(中、右)所示。

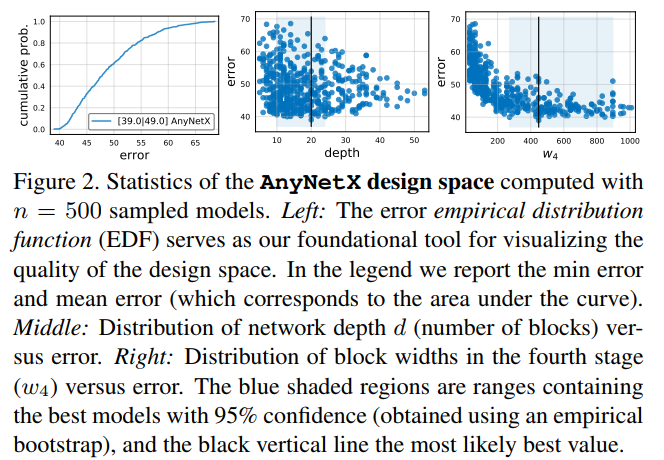
补充：给定$n$对$(x_i,e_i)$，其中$x_i$表示模型的一个属性如depth，$e_i$表示对应的模型误差。通过如下步骤完成empirical bootstrap。

从这$n$对中随机采样25%，得到一组sample
选择这一组sample中误差最小的一对
重复这个步骤$10^4$次
计算这$10^4$对样本属性$x$的95%置信区间，并以中位数给出了最优可能的值。

置信区间理解：以相同的抽样方式，获得N组抽样样本，每一组抽样样本点数为M，对于每一组抽样样本，按某一置信度，比如说95%，计算出置信区间，那么将会有0.95*N组所计算出来的置信区间中包含有总体待估计参数值。
不同的样本集具有不同的置信区间，置信区间是随机变量。那么，求某一个样本集的置信区间究竟有什么意义呢？在实际应用中，当我们需要研究总体的某些特征时，以总体的均值为例，由于无法获得全体数据，我们通过采样来获得一组样本，这组样本均值作为总体均值的一个点估计，而这组样本的置信区间作为总体均值的一个区间估计。这里以95%置信度为例，那么由这组样本计算出来的95%置信区间能够说明什么呢？通过实验，采样1000个样本集，则可以计算出来的1000个置信区间，其中有大约950个置信区间包含有真实值，换句话说，假设置信区间为[a,b]，选置信区间的目的是为了让“a和b之间包含总体平均值”这一结果具有特定的概率，这个概率就是置信水平，并不是说总体待估计参数（比如说均值）以一定的概率落在置信区间内。。所以利用置信区间可以一定程度上对于真实值的取值范围有所了解。

总结来说：

作者从一个设计空间中采样并训练$n$个模型
计算并画出决策空间的EDFs来表征设计空间的质量
使用empirical bootstrap来对一个设计空间的不同属性进行可视化
根据可视化结果来调整设计空间

The AnyNet Design Space

在本文中，一个网络中的元素包含如下几个部分：

blocks的数量（即网络深度）
block的宽度（即channels的数量）
其它的block参数，例如bottleneck ratios or group widths

初始的AnyNet设计空间很直观，给定一张图片，一个网络由一个simple stem，紧跟着一个执行大量计算的boby部分，最后是预测输出类别的head网络。如图3a所示。作者让stem和head部分尽可能的简单，并且保持固定。然后主要聚焦在网络的boby部分。

boby部分由4个stage组成（在3.4节探讨了stage的变化），逐渐降低特征图尺寸，如图3b所示。每一个stage都包含相同的blocks，如图3c所示。对于stage $i$，自由维度包含blocks的数量$d_i$，block的宽度$w_i$，以及其他的block参数。虽然整体结构比较简单，但是AnyNet中可能网络的总体数量是巨大的。

作者大部分实验都是在有分组卷积的标准residual bottlenecks block上进行的，如图4所示。作者将这种block称为x block，基于该block的设计空间为AnyNetX（作者在3.4节探索了别的blocks）。

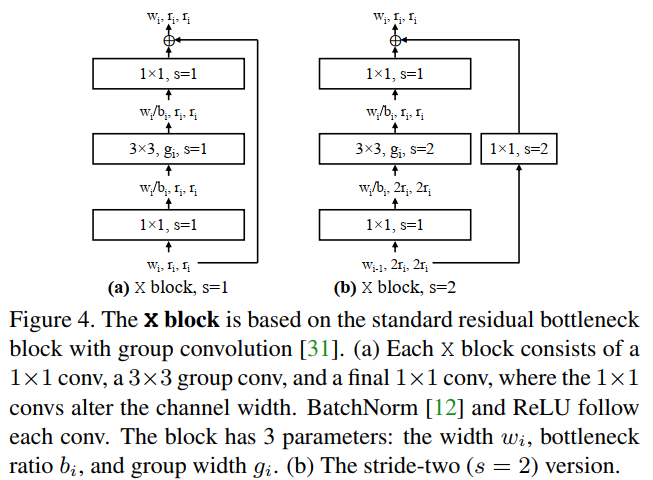
AnyNetX有16个自由维度——4个stage，每个stage都有blocks的数量$d_i$、block的宽度$w_i$，bottleneck ratio $b_i$, and group width $g_i$。作者固定了输入分辨率$r=224$。为了更好的采样，规定$d_i\leq 16,g_i \in \{1,2,\cdots 32 \}$，$b_i \in \{1,2,4\}$，$w_i \leq 1024$且能被8整除。重复采样直到采样到500个满足FLOPs落在300MF到400MF的模型，然后训练10个Epoch，根据作者的经验，10个Epoch已经足够能给出具有鲁棒性的设计空间统计。AnyNetX的基本统计在图2中给出。

若使用NAS的方法，会在这$(16\cdot 128 \cdot 3 \cdot 6)^4=10^{18}$个模型中搜索出一个最优模型。但是作者借助上面的设计空间评价工具探索一般的设计原则，从而更好的理解和调整设计空间。在这个过程中，目标是：

简化设计空间
提高设计空间的可解释性
提高或者保持设计空间的质量
保持设计空间的多样性

主要的步骤如下：

AnyNet$X_A$：为了下面表述清晰，作者将上面的AnyNetX空间表示为AnyNet$X_A$。

AnyNet$X_B$：对于AnyNet$X_A$设计空间中的所有的stage $i$都采用同一个bottleneck ratio $b_i=b$，得到新的设计空间为AnyNet$X_B$。AnyNet$X_A$和AnyNet$X_B$的EDFs曲线如图5左所示，可以看到两者曲线基本保持一致，也就是说当所有的stage $i$都采用同一个bottleneck ratio时，网络精度并没有损失。这样处理除了简化了设计空间之外，AnyNet$X_B$更容易分析，如图5右所示，$b$的95%置信区间为$b\leq2$，但是AnyNet$X_A$并没有这样的趋势（并没有给出图）。

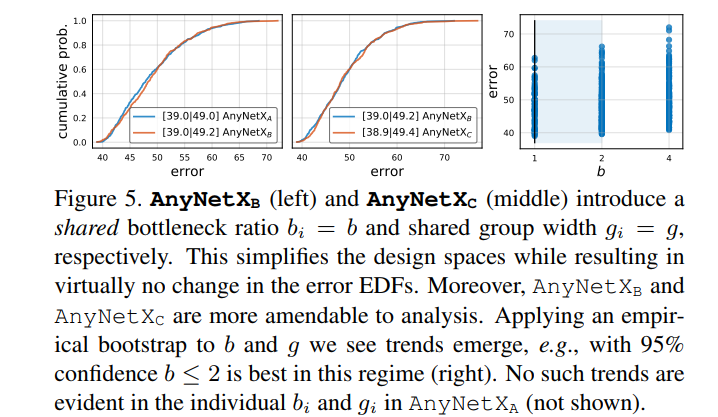
AnyNet$X_C$：在AnyNet$X_B$基础上，在进一步保持各个stage $i$都采用同一个group width $g_i=g$，得到新的设计空间为AnyNet$X_C$。如图5中所示，当所有的stage $i$都采用同一个group width时，网络精度并没有损失。这样就可以进一步简化设计空间，AnyNet$X_C$比AnyNet$X_A$减少了6个自由度。另外，作者发现当$g > 1$时是最优的（实验没有展示出来），这部分在第4节进行详细介绍。

AnyNet$X_D$：接着作者对AnyNet$X_C$中的最好的结构（图6上）和最差的结构（图6下）进行了分析。图中，横坐标表示每个block $j$下标索引，而纵坐标表示每个block $j$对应的网络宽度$w_j$，$d_i$表示第$i$个stage有多少个block，而$w_i$表示第$i$个stage的网络宽度（每个stage内部网络结构相同）。例如下面第一幅图就表示，第一个stage有一个block，宽度为48；第二个stage有2个block，宽度为80；以此类推。

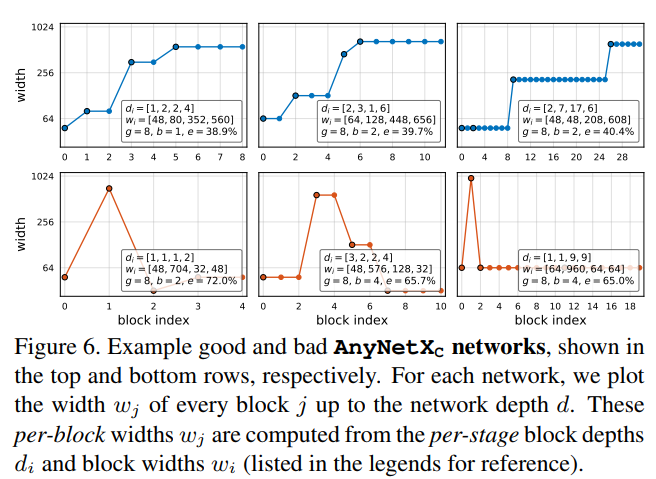
然后可以发现好的网络都有一个共同的属性，网络的宽度逐渐增加，也就是说$w_{i+1} \geq w_i$，有该约束的设计空间称为AnyNet$X_D$。画出该空间的EDF曲线，如图7(左)所示，发现通过该原则，能够极大的提高EDF。

AnyNet$X_E$：通过观察更多的模型（并没展示出来），作者发现对于比较好的模型，每一个stage的宽度$d_i$也有逐渐增加的趋势，但是最后一个stage并不需要。虽然如此，作者约束$d_{i+1} \geq d_i$得到新的设计空间AnyNet$X_E$，然后画出该空间的EDF曲线，如图7(右)所示，发现通过该原则，也能提高EDF。

靠着一步步的优化，缩小设计空间，作者最终得到了大量包含优质模型且设计空间较小的AnyNet$X_E$。

The RegNet Design Space

为了更好的理解模型结构，从AnyNet$X_E$中选出最好的20个模型，然后画出来每个block $j$的网络宽度$w_j$和每个stage $i$的网络深度$d_i$，如图8左上所示。

虽然每个模型之间的差异巨大，但是整体上表现出来了一种趋势，即当$0\leq j \leq20$时，有$w_j=48 \cdot (j+1)$，也就是图8左上图中的黑线，值得注意的是，纵坐标是取log后的。但是这种量化方式，对于每一个block $j$都指定了一个特定的宽度$w_j$，但是实际上不同模型的$w_j$是不同的，另外若采用这种量化方式，也没有办法保持设计空间的多样性。

为了解决这个问题，作者采用了下面的改进思路：

为每一个block的宽度引入一个线性参数化的方程：

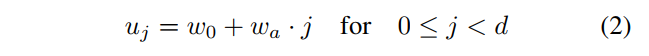
该方程有三个参数：深度$d$，初始宽度$w_0>0$，斜率$w_a>0$。通过该方程为每一个block $j0$，用于计算量化因子$s_j$。量化过程如下：

简单地说就是算出来的宽度可能是126.123之类的奇葩数字，得给它四舍五入到128这种科学的数字，同时每个stage $i$有很多block，得把宽度统一到某个数字。这就需要拿一个分段函数去近似上面的线性函数。于是就有了下面的步骤。
$w_0、w_a、w_m$都是有自己取值范围的，实际使用时会采用网格搜索的方法，因此在理解这些方程时可以将其看做是常数。

首先给定一个方程(2)中的$u_j$，计算出每一个block $j$的$s_j$：

然后，对$s_j$取整用$\lfloor s_j \rceil$表示，然后将量化后的$s_j$带入式子(3)即完成对$u_j$量化，得到每一个block的实际宽度$w_j$，用下式子表示：

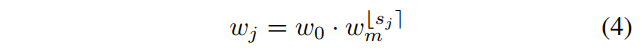
接着将每个block的宽度转换为stage的形式，也就是说。每一个stage $i$的block宽度为$w_i=w_0 \cdot w_m^i$，block的数量为$d_i = \sum_j \mathbf{1} \left[ \lfloor s_j \rceil = i\right]$（因为量化因子$s_j$控制了block的宽度，同一个stage中block的宽度相同，因此也就有了这两个公式）。

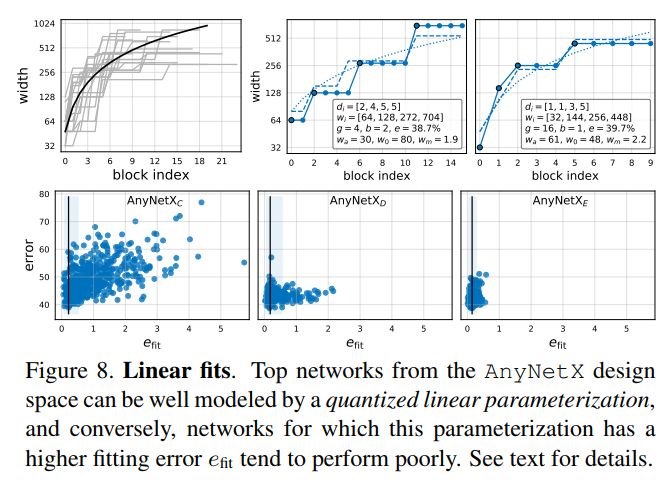
在AnyNetX空间验证这种参数化的方法。也就是说，给定一个模型，设置网络的深度为$d$，网格搜索得到一组参数$w_0,w_a,w_m$，使得使用该组参数预测出的模型和实际给定的模型每一个block宽度之间的差异最小。该差异用$e_{fit}$表示。AnyNet$X_E$中的两个最好的模型如图8(上中右)所示。可以看到量化后的函数(虚线)和这些模型(实线)拟合的很好。

接下来，我们画出拟合误差$e_{fit}$关于AnyNet$X_c$到AnyNet$X_E$中模型的曲线如图8(下)所示。

首先，观察到设计空间中最好的模型都有很好的拟合度。通过empirical bootstrap方法发现，$e_{fit}$值接近零的一个窄带，可能包含每个设计空间中的最佳模型。
然后，可以发现从AnyNet$X_c$到AnyNet$X_E$，$e_{fit}$越来越小。

为了进一步测试这种线性参数化的方法，基于AnyNet$X_E$限制$d<64$，$w_0,w_a<256$，$1.5\leq w_m \leq3$，$b$和$g$与之前介绍的方式相同，在这个范围内采样，利用公式(2)-(4)得到具体的网络结构。称有这种限制的空间为RegNet，它只包含简单的、常规的网络。

RegNetX的EDF如图9(左)所示，可以看到RegNetX中的模型的平均误差比AnyNetX小，说明RegNetX中的模型都是比较优秀的模型。

从图9(中)作者进一步的对参数进行了限制，具体而言：

使用$w_m=2$（也就是stage之间的block宽度翻倍）轻微的提高了EDF，但是$w_m \geq 2$表现更好（后面展示）。
测试了$w_0=w_a$，进一步简化线性参数化方程为$u_j = w_a \cdot (j+1)$。这样效果也变得更好了。

但是为了维持模型的重要性，作者并没有采样这两种限制。图9(右)展示了随机搜索的效率，发现RegNetX搜索大约32个模型就有可能产生好的模型。

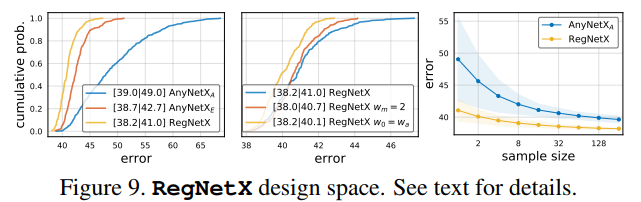
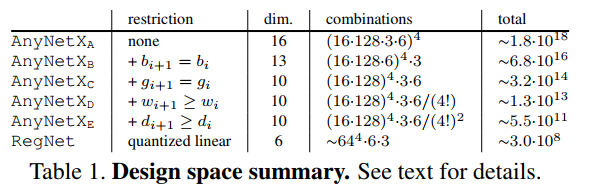
表1展示了决策空间尺寸的摘要。从原始的AnyNetX设计空间到RegNetX设计空间，作者将自由维度从16缩小到了6，空间缩小了约10个数量级。然而RegNet仍然包含了设计空间的多样性。

Design Space Generalization

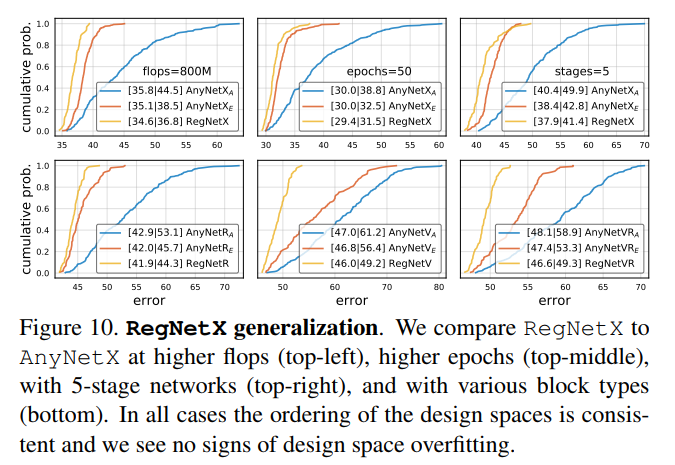
我们设计的RegNet设计空间是在low-compute, low-epoch的训练模式下进行的，只有一种block 类型。然而，我们的目标不是为单一设置设计一个设计空间，而是发现可以推广到新设置的网络设计的一般原则。

在图10中，我们在higher flops, higher epochs, 5个stage, 不同种类的block类型下比较了AnyNet$X_A$、AnyNet$X_E$和RegNetX设计空间。在各种模型下，都有RegNetX>AnyNet$X_E$>AnyNet$X_A$。换句话说，我们的规则并没有在特定的设置上过拟合，具有一定的泛化能力。

Analyzing the RegNetX Design Space

接下来进一步分析RegNetX设计空间，重新探讨深度网络设计的一些通用规则。RegNetX设计空间有大量的优秀模型，接下来的实验我们改为采样更少的模型（100）个，训练的epoch增多一点（25个）。这样就能观察到更加精细化的趋势。

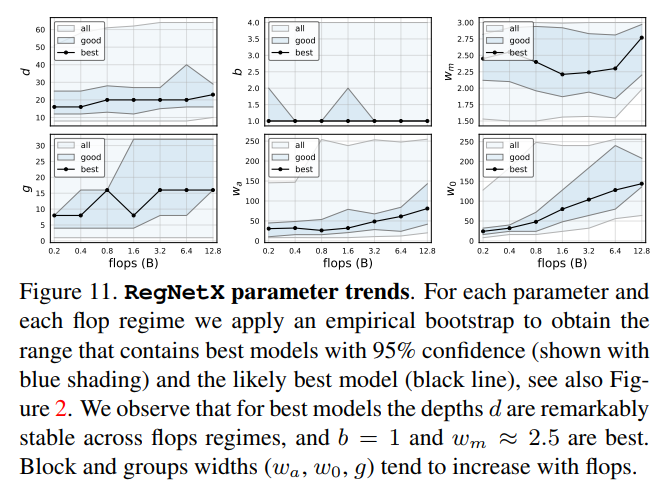
RegNet trends. 图11中展示了RegNetX在不同FLOPs下各种参数的趋势。值得注意的是，通过图11(上左)，发现在不同FLOPs下最优模型（黑色的线，使用empirical bootstrap得到）的depth都很稳定，大概为20个blocks（60层）。这与实际实践中，通常使用更深的模型以得到更高的FLOPs形成了鲜明的对比。通过图11(上中)，发现最优模型的bottleneck ratio $b=1.0$。通过图11(上右)，观察到优秀模型的乘子$w_m$是2.5。这与实际经常采用的stage之间宽度翻倍的方式有点相似但是不完全相同。剩余的参数（$g、w_a、w_0$）随着复杂度的增高而增加。

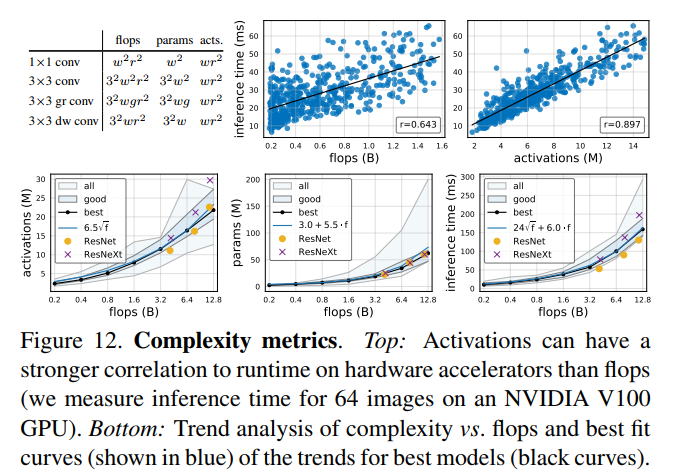
Complexity analysis. 除了FLOPs和参数，作者分析了所有卷积层的输出tensor的尺寸，将其定义为network activations，用于度量网络的复杂度，在图12的左上角列出了常见卷积算子的复杂性度量。虽然activations不是衡量网络复杂性的通用标准，但activations可能会严重影响内存受限硬件加速器(例如GPU、TPU)上的运行时间，在图12(上)可以看到，activations跟推理时间的正相关性比FLOPs更强。在图12(下)中，观察到对于总体中最好的模型，activations随FLOPs的平方根增加，参数量随FLOPs线性增加，并且推理时间最好使用FLOPs的线性和平方根项联合建模（即图12(下右)中的式子$24 \sqrt f + 6.0 \cdot f$），因为它同时依赖于FLOPs和activations。

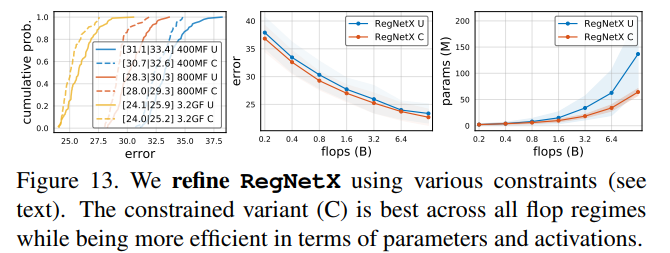
RegNetX constrained. 使用上述这些发现，我们可以对RegNetX设计空间进一步微调，首先基于图11(上)，设置$b=1,d\leq40,w_m\geq2$。然后基于图12(下)，对参数量和activations进行约束。这样就能产生快速的、低参数量的、low-memory且不影响精度的模型。在图13中，我们对比了RegNetX有这些约束和没有这些约束下的表现，可以发现在所有FLOPs下，有约束的性能比没有约束的更好。因此在下面的实验结果小节都使用有约束的版本，然后更进一步的限制网络深度$12\leq d \leq 28$（在附录D中有解释）。

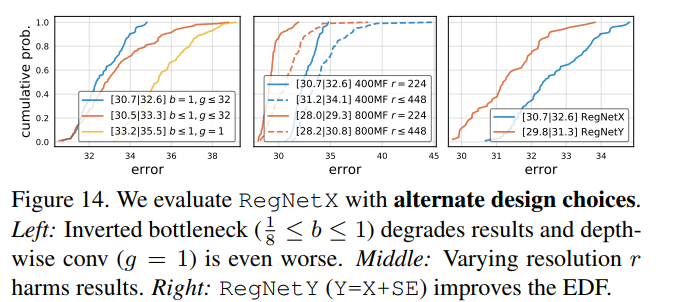
Alternate design choices. mobile network经常采用the inverted bottleneck (b < 1) 和depthwise conv。在图14(左)，观察到相对于$b=1, g\geq 1$，inverted bottleneck轻微的降低了EDF，depthwise conv（group width $g_i=1$）表现更加差劲。接下来，作者测试了在不同输入图像分辨率对网络的影响，如图14(中)所示，与一般的结论相反，即使在更高的FLOPs，将RegNetX的分辨率固定为$224 \times 224$表现更好。

SE. 最后，作者将block X和SE模块进行结合，得到了新的设计空间RegNetY。在图14(右)，发现RegNetY性能提升比较明显。

实验结果

作者将RegNetX和RegNetY中的最优模型和目前State-of-the-art模型在各种FLOPs下进行对比。对于每一个FLOPs，作者从设计空间中选取最优模型，然后重新训练100个Epoch。在不同FLOPs下，RegNetX和RegNetY中的最优模型结构在图15和16中给出。除了在上面第4章分析出的结论外，作者还发现了如下结论：

更高FLOPs的模型在stage 3中有更多的blocks，但是在stage4有更少的blocks，这和标准的ReNet网络设计相似。
group width随着$g$的模型复杂度的提高而增加，但是depth $d$会饱和。

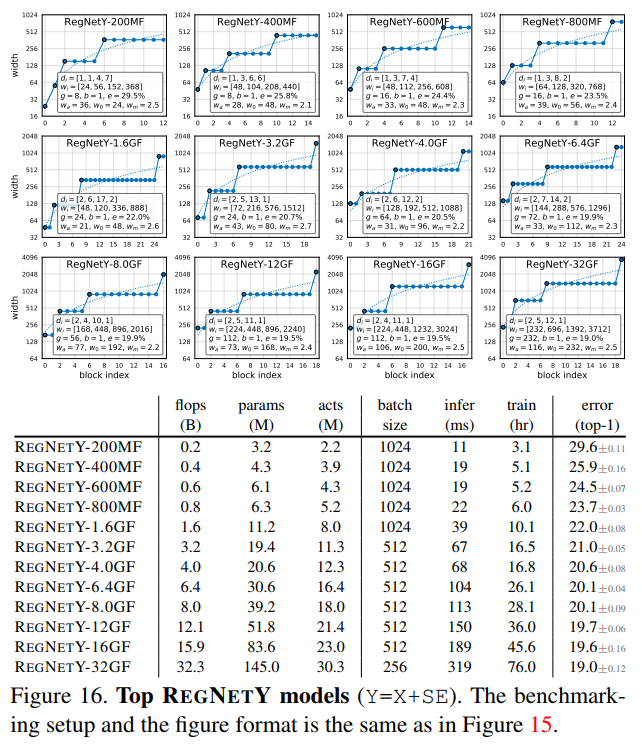
为了公平的比较模型结构带来的差异，作者在训练网络的时候关掉了所有的增强方式。

State-of-the-Art Comparison: Mobile Regime

对于移动端，更加关注在600MF下模型的表现，作者比较了600MF RegNet模型和现有的mobile网络。发现不管是人工设计的网络还是NAS搜索出的网络，都没有从RegNet选出的模型精度高。

Standard Baselines Comparison: ResNe(X)t

作者将RegNet网络和标准的ResNet、ResNext网络进行对比。对比结果在图17和表3中给出，可以发现只通过优化网络结构，RegNet可以取得巨大的提升。表3(a)比较这些方法时采用的是根据activations进行分组，在给定固定推理时间或训练时间下，RegNetx模型都非常有效。

State-of-the-Art Comparison: Full Regime

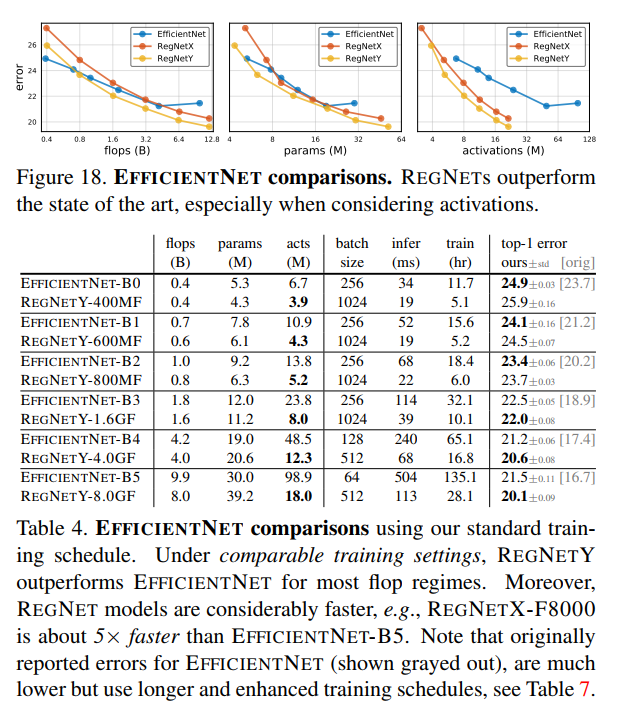
作者将EfficientNet和RegNetX、RegNetY进行比较，并控制两者在训练过程中参数一致。结果在图18和表4中给出，可以发现，在较低FLOPs下，EfficientNet表现比较好，但是在中等FLOPs下，RegNetY表现比EfficientNet好，在较高FLOPs下，RegNetX和RegNetY表现都比EfficientNet好。

还可以观察到，受到同时对分辨率和深度进行scale的影响，EfficientNet的activations随着FLOPs线性增长，而RegNet的activations随FLOPs的平方根增长。这导致了EfficientNet的GPU训练速度和推理速度较慢，例如RegNetX-8000比EfficientNet的推理时间快了5倍，同时错误率更低。

Additional Ablations

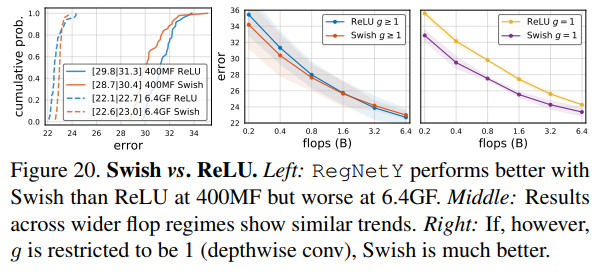
最近的很多工作使用了swish激活函数，在图20中，作者对比了RegNetY在Swish and ReLU不同激励函数下的性能，发现swish激励函数在低FLOPs下表现更好，而ReLU激励函数在高FLOPs下表现更好。如果$g$被约束到$g=1$（depthwise conv），那么swish函数比relu函数表现更好，也就是说swish函数和depthwise conv更加搭配。

总结

使用NAS虽然可以产生优秀的网络，但是有着固有的缺点：

搜索空间大，特别消耗GPU资源
换一种空间或者设定，又要重新开始搜，不具有通用性
不具有通用解释性

而手动设计的网络性能通常没有NAS搜索出来的好，但是可解释强，有通用的网络设计规则。

面对这些问题，作者将NAS和手动设计网络相结合，从统计学的角度出发，对网络设计空间进行整体估计。从整体估计中，一步步发现网络设计的规则，对设计空间进行优化和限制，提高了模型搜索的速度和效果。然后，作者将该规则应用到higher flops, higher epoch, 5个stage, 不同的block类型的设计空间上，验证了这些网络设计规则具有泛化能力，并不是针对某个设置而言的。最后说明了，在相同的FLOPs和训练参数下，RegNet模型比EfficientNet的性能更好且在GPUs最多提速5倍。

补充

以下内容来源于FLOPs与模型推理速度。

大家都知道EfficientNet论文以大幅度降低FLOPs为卖点，但是其推理速度却很慢。比如B3版本的FLOPs不到ResNet50的一半，推理速度却是ResNet50的两倍。那么FLOPs与模型推理速度之间有什么关系么？

大部分时候，对于GPU，算力瓶颈在于访存带宽。而同种计算量，访存数据量差异巨大。

而EfficientNet就是使用了大量的低FLOPs、高数据读写量的操作，更具体来说，就是depthwise卷积操作。这些具有高数据读写量的操作，加上GPU的访存带宽限制，使得模型把大量的时间浪费在了从显存中读写数据上，GPU的算力没有得到“充分利用”。上面其实这个activations大小，就可以看作模型进行推理时，需要从显存中读取的feature blob的大小，近似可以认为是访存数据量的大小。那么我们不妨从activation这个角度看看EfficientNet，看看depthwise卷积与普通卷积的区别。二者在同等FLOPs下，activation有什么不同？这种不同为什么又会导致推理速度的不同？

说depthwise的高数据读写量不是指从CPU往GPU拷贝数据的过程。GPU本身有储存单元和计算单元。这里的数据读写，是指GPU把显存里的数据，从储存单元读取，写入到计算单元（GPU Cores）计算的过程。一块P40，24G显存，可不是这24个G都是计算单元。

为简化处理，以下内容只计算乘法，不计算加法。

假设一个大小为56*56*100的feature（$HWC$），经过一个kernel size为3x3的普通卷积layer，卷积layer的输出channel也是100，输出特征图大小也是$56 56 100 $。其FLOPs计算过程如下：

一个卷积kernel的大小为：$33100$，与feature上一个同等大小的blob进行卷积，这是一个逐元素点乘操作，总共有$33100$次乘法。然后卷积layer输出channel是100，说明有100个这样的卷积kernel，同时在feature的空间位置上，每个像素点都要重复一次卷积操作，共$5656$次，所以总的FLOPs为：**3\3*100*100*56*56。卷积核参数总量为：3*3*100*100**。

然后为了达到同样的FLOPs，我们假设另一个大小为56*56*10000的feature，经过一个kernel size为3x3的depthwise卷积layer，卷积layer的输出channel是10000，输出特征图大小也是$56 56 10000 $。其FLOPs计算过程如下：

一个卷积kernel的大小为：$331$，与feature上一个同等大小的blob进行卷积，总共有$33$次乘法。然后10000个channel通道，每个通道互相独立，对应着10000个不同的卷积kernel，所以重复这一卷积过程10000次。同时在feature的空间位置上逐元素重复，总的FLOPs为：**3\3*10000*56*56。卷积核参数总量为：3*3*1*10000**。

可以看到，两个layer的FLOPs和参数量完全相同。但是推理速度方面，depthwise卷积要远远慢于普通卷积。其原因就是访存数据量的不同：

由于卷积计算本身已经是flatten的，不需要考虑重复读取问题，那么总共读取的数据量就是feature的大小加上卷积核weight的大小，对于普通卷积来说，总读取数据量为：$1005656 + 33100100 = 4.0e+05$。类似的，depthwise卷积读取的数据总量为：$565610000 + 33*10000 = 1e+07$

可以看到，在同等FLOPs的情况下，depthwise卷积对应的feature size比普通卷积大的多，受制于GPU访存带宽，过高的数据读取与写入量就成为了限制推理速度的瓶颈。

我们再回头看EfficientNet，不难看出其中的“取巧”成分。数据访存量与feature size（RegNet中的activation）有关，而feature size又与空间尺寸以及channel通道数（或者换句话说，网络的宽度width）有关。EfficientNet的一个核心就是增大空间尺寸或者网络宽度width以提升模型精度。

由于depthwise卷积的存在，增大feature的空间尺寸，或者channel通道数（width）都不会显著地增加FLOPs。因此EfficientNet可以声称自己是低FLOPs，但不得不说，这是一种“FLOPs假象”。因为feature size的增大会增加数据访存量，进而增加模型推理时间，这是单纯的FLOPs反映不出来的。

另外，轻量型的网络中大多都使用了depthwise卷积是出于怎样的考虑，是不是因为在计算受限制的硬件上，普通卷积的网络和depthwise卷积的网络都能达到硬件计算瓶颈的情况下，访存量就没这么重要，模型的FLOPS主要决定了推断时间的多少？

答：首先，直观上也倾向于计算瓶颈更占主导地位；

其次，现实应用中，“真正”用于移动终端的轻量级网络使用depthwise的逻辑是这样的，它们的网络一般和标准ResNet“差不多宽”，或者更小。在这种情况下，depthwise的FLOPs和数据访存量（因为depthwise至少参数量小）都会比普通卷积小，这种情况下自然是很快的。

最后，FLOPs“诡计”特指那些在ImageNet上用V100刷榜的文章，为了保持FLOPs低，采用了depthwise这样的结构，然后为了刷榜，不得不把输入变大、把网络加宽，然后使用各种很耗时的attention，比如$x=x*sigmoid(x)$。用“FLOPs低”这样的装饰说辞，说自己Efficient。这背后的逻辑应该是，同等宽度下（注意不是FLOPs，可以近似理解为同等数据访存），对于复杂/困难任务，depthwise卷积的快，一定是带来了性能的损失，因为丧失了“更多的可能性”，depthwise毕竟是普通卷积的一个子集。精度损失在移动端可以接受，在ImageNet刷榜就不能接受了，才要另辟蹊径。